中国人民大学健康大数据研究院李扬教授团队系列自适应设计成果在多份期刊《Statistica Sinica》《Biometrics》《Computational Statistics & Data Analysis》《Statistics in Medicine》接收发表。

随机对照试验（RCT)是检验干预措施效果的金标准，被广泛应用于药物疗效评价、政策效果评估等领域。2019年，诺贝尔经济学奖授予三位科学家，表彰他/她们运用RCT“在减轻全球贫困方面的实验性做法”。传统RCT采用固定随机概率的完全随机化方法，简单易行，但伴随临床实践发展面临诸多挑战。例如，完全随机化方法往往无法有效平衡多种治疗间的协变量，导致疗效估计的有效性降低；也无法最大化受试者的利益，即无法将更多的受试者随机分配到治疗效果更好的干预组中。自适应设计基于累积的试验数据动态调整随机策略，使试验更加灵活、高效且合乎伦理，还能减少试验时间和成本。近年来，自适应设计在制药行业得到了广泛应用。例如，在ESCAPE 试验（NCT01778335）中，研究者使用协变量调整自适应随机化（CAR）实现了在小样本情形下多基线协变量的组间平衡，增强了分析的可信度，提高了统计效率。

中国人民大学健康大数据研究院李扬教授团队围绕“如何在临床试验自适应分配过程中实现影响因素的平衡”这一主题，在不同应用场景下分别提出了ARM、SARM、ARMM等自适应方法，并将受试者间的非独立关系纳入考虑，提出了NCARA。数值分析与理论分析显示，上述方法在平衡影响因素、提升估计有效性等方面表现优秀，并在CANTATA-SU（NCT00968812）、The Kanyakla Study（NCT02474992）等实证数据分析中得到印证。相关成果已发表于Statistica Sinica、Biometrics、Computational Statistics & Data Analysis、Statistics in Medicine等期刊。

一、Adaptive Randomization via Mahalanobis Distance（ARM）

挑战：完全随机化等分配方法往往无法有效平衡治疗组间的协变量，并且随着协变量数量的增加，这种不平衡问题会愈加严重。在一项使用Ceragem热疗按摩床治疗腰椎间盘疾病的临床研究中，186名患者被随机分配到试验组或对照组，两组间的马氏距离为57.815，这表明组间协变量失衡，可能导致疗效估计的方差过大。

ARM使用马氏距离衡量组间协变量的不平衡程度，每当两个受试者进入试验时，该方法将更倾向于选择使马氏距离最小的分配方案。经过理论、数值模拟以及真实数据分析，该方法较之其他竞争方法展现了诸多优点：

• 协变量的不平衡程度随样本量的增加趋于0；

• 计算时间仅随n线性增长且几乎不受p的影响，优于重随机化的指数增长；

• 疗效估计渐近地达到最小方差，使统计检验在竞争方法中达到最高功效。

图1 对于不同的样本大小 n 和协变量数量 p，使用 ARM和重随机化获得的马氏距离的分布。不难发现，ARM的马氏距离一般情况下小于重随机化，即ARM有更好的协变量平衡效果。

图2 两治疗组总体均值差的统计检验的功效。样本量 n = 5000。从左到右是四个工作模型。不同随机化方法的结果，CR、RR、ARM、mARM、DA-BCD、CA-BCD、SPBR 和 SBCD 显示在每个子图中。不难发现ARM的功效始终是最高的。

二、Sequential Adaptive Randomization via Mahalanobis Distance（SARM）

挑战：尽管许多理论上合理的自适应随机化方法实现了协变量平衡，但他们通常要求所有患者在分配之前全部可获得，或者将患者成对或分组分配，这影响了随机化方法在临床上的实践，此外，如果患者以个体为单位被序贯地分配，那么试验组和对照组之间样本量的平衡可能无法保持。

SARM以患者个体为单位进行序贯分配，并分离了协变量不平衡（通过修正的马氏距离来衡量）和边际不平衡（即两组之间的样本量差异），即只有当边际不平衡被控制在理想水平时，所提出的方法才能最小化协变量不平衡。经过理论、数值模拟以及真实数据分析，该方法较之其他竞争方法展现了诸多优点：

• 满足了每个患者入组后立即分配的实际需求；

• 在保持边际平衡的同时实现了最佳协变量平衡；

• 在协变量平衡和疗效估计等方面具有与ARM方法相同的理想性质。

图3 不同方法下马氏距离和绝对样本量差异的比较。M-distance为试验结束时试验组和对照组的协变量均值向量的马氏距离，|n₀-n₁|代表试验组和对照组的样本量差异。不难发现，SARM（即图中的SCR）在协变量平衡与边际平衡上优于其他竞争方法，甚至在样本量较少时，在样本量平衡方法要优于ARM。

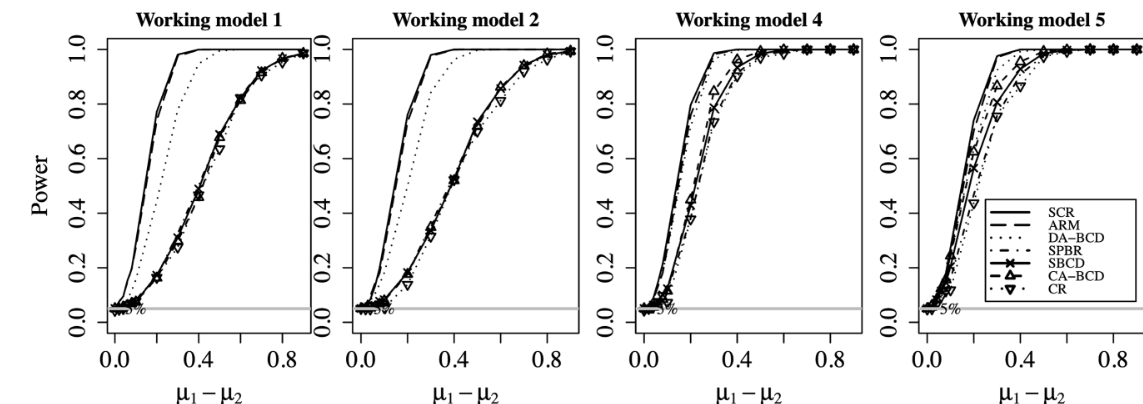
图4 两治疗组总体均值差的统计检验的功效。样本量 n = 1000。从左到右是四个工作模型。不同随机化方法的结果，SARM（即图中的SCR）, ARM, DA-BCD, SPBR, SBCD, CA-BCD, 和CR 显示在每个子图中。不难发现SARM和ARM的功效始终是最高的。

三、Adaptive Randomization via Mahalanobis Distance for Multi-arms（ARMM）

挑战：多臂试验在医学和健康研究中很常见。与板块1中的问题类似，虽然确保协变量平衡是比较研究成功的关键所在，但经典的多臂试验（例如完全随机化）往往无法平衡多个治疗组之间的协变量。

ARMM方法解决了多臂情景下的协变量平衡问题。ARMM是ARM在多臂情形下的推广，每当K（即，治疗组数量）个受试者进入试验时，该方法将更倾向于选择使马氏距离最小的分配方案。经过理论、数值模拟以及真实数据分析，该方法展现出了与ARM相同的优点：

• 协变量的不平衡程度随样本量的增加趋于0；

• 在计算时间上较之重随机化具有明显优势；

• 疗效估计渐近地达到最小方差。

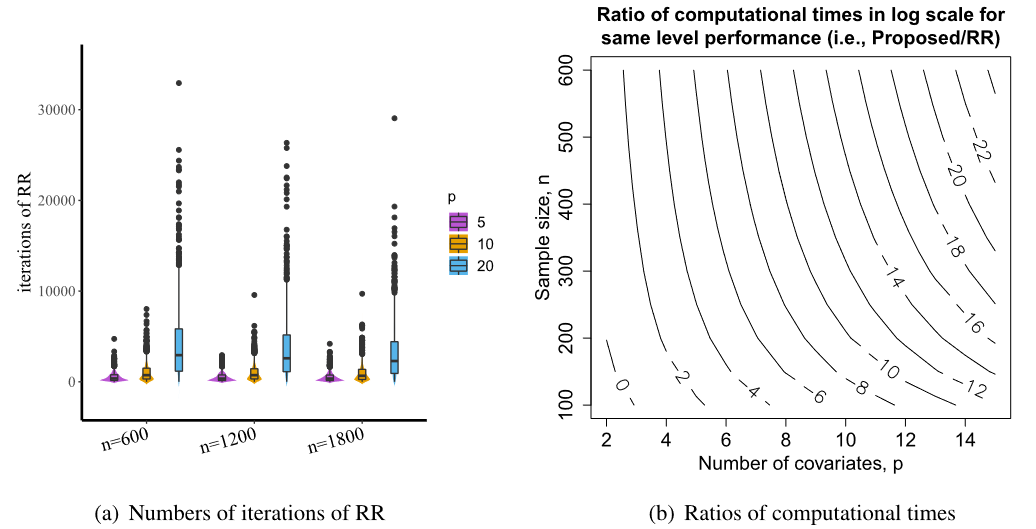
图5 不同样本量n和协变量数量p下，重随机化（RR）的迭代次数与计算时间比率的比较。图（a）：Pa = 0.05 时，RR所需的迭代次数。图（b）：实现相同性能（即相同的马氏距离）所需的 ARMM 与 RR 的计算时间之比的对数，即log（ARMM/RR）。由图（a）可知，RR所需的迭代次数随p的增加呈指数增长。由图（b）可知，在达到相同性能的前提下，log（计算时间的比率）随着p或n的增加迅速接近0。这意味着在大样本和高维情形下，RR在实际操作中不可能达到与ARMM相同的性能。

四、Network Covariate-balanced Response-adaptive Randomization（NCARA）

挑战：在部分临床试验中，各个患者的结局可能会相互影响，这要求在试验设计中考虑患者间的网络关系。例如，在孟加拉国农村进行的一项评估霍乱疫苗与安慰剂的保护效力的试验中，霍乱感染的可能性受到改变个人接触率的社会和行为因素的影响。忽略这些来自人们社会关系的干扰会导致估计的偏差。

NCARA在确保重要协变量的组间平衡并将更多患者随机分配到疗效更优的治疗组的同时，平衡了治疗组之间的网络关系，同时满足了研究者的三个需求。该方法有如下优势：

• 三个方面的总体表现优于所有替代设计（RAR、NAR、CAR 和 CR）；

• 在一些特定网络结构下，疗效估计的偏差比替代设计更小；

• 在样本量较小和网络干扰较大的情形下，NCARA的优势将进一步凸显。

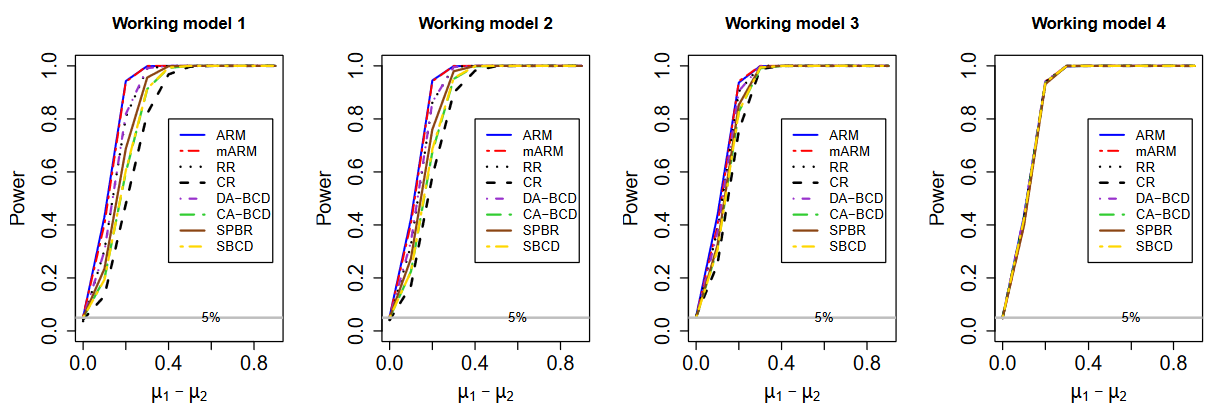
图6 不同网络干扰水平下随机化设计的功效：网络和协变量调整响应自适应设计的功效用实线连接的红色方块绘制，替代设计的功效用不同颜色和不同符号的虚线表示。ER、BA、SB、WS分别代表四种不同的网络结构。从图中可以看出，在所有网络结构下，网络干扰的增加显著地降低了功率，但NCARA和NA表现出相对更好的性能；样本量越小，网络干扰程度越高，NCARA的优势越大。